蜗牛扑克allnewpoker『www.allnew366.com』亚洲唯一代理,注册登陆游戏访问更快,存提款更加方便,提供安卓苹果APP客户端下载,合法安全稳定,在线中文客服为您服务
发布时间:2021-04-20 文章来源:蜗牛扑克
分布游戏
这里是我们第一次介绍[0,1]分布游戏。第三部分里,我们会讨论许多使用这个分布的游戏。在[0,1]游戏里,两名玩家都被发到一个均匀分布的随机实数。这意味着两个玩家有相同的概率被发到任何一个0,1之间的数字。这些数字对于玩家而言类似扑克的手牌。这里我们的规则是,如果有摊牌,那么数字最小的获胜(为了简化计算)。意味着0是最强牌,越靠近0越强,而1是最弱牌,越靠近1越弱。
这类游戏的策略与之前先知游戏有完全不同的结构。最主要的区别是,并不严格要求混合策略。因为手牌的数量是无限的,混合任意一手牌都不会影响。而对于任意间隔而言,我们都可以更有效地使用单纯策略,通过设定一个阈值。0,1之间连续区域的边缘点标志了不同的动作。
当解决[0,1]游戏时,我们会经常用到下列技巧:
1) 猜测答案的结构
2) 按照猜测的结构去解决游戏
3) 通过检查玩家是否可以单边提高期望来验证答案是否正确
我们把这个猜测答案结构的过程叫做参数化。比如,[0,1]游戏一个可能的答案是Y下注最好的0~y1之间的手牌,然后过牌y1到y0之间的手牌,下注y1~1之间最差的牌。其他的参数化可以是Y下注中等强度的手牌,过牌最好和最差的牌。有许多种结构的答案都可以;如果我们猜测一种,就可以继续解决那种。
一旦我们确定了一种参数化,剩下就是找到最优答案。我们根据无差别的原则建立出方程。相对于之前混合手牌范围需要的无差别,我们在这里找出分割动作的阈值,让对手无差别。
这里正确的原因也许并不明显,有一些直观的论据:首先,我们知道如果我们沿着直线上移动非常小的距离(从一手牌到略强的一手牌)我们的摊牌赢率是连续的,也就是说,一手牌摊牌赢率和他附近邻居的值非常接近。如果这样的话,那么玩这手牌的价值也是连续的。因为价值是由摊牌赢率和非摊牌赢率构成(而非摊牌是一个常数)。比如,过牌跟注手牌0.6的价值应该跟过牌跟注0.60001的价值非常接近。现在我们考虑价值的阈值,假设某一选项在阈值的赢率高于其他选项。那么在低价值区域里,我们会找到一小部分非常接近阈值,从而可以切换到高价值区域,并获得赢率。如果我们可以这么做,那么策略就不是最优的。因此最优策略在阈值是无差别的。
在我们大多数的参数化中,我们有固定数量的阈值(在不同策略就间)。对于每一个阈值,我们写一个关于策略元素的方程使阈值无差别,称之为无差别方程。通过解这些方程组,我们可以找出每个阈值,并且找出每组参数的最优策略。
有些情况下,通过不同的参数化组合可以找到更好的策略。通常,如果我们通过错误的特定参数化列出方程,那么我们会碰到不连续(比如不可能的阈值)。因此我们在解决特定参数化之后必须要确认这些策略,从而验证的确是最优策略。
牌例 11.2 – [0,1]游戏 #1
这是个非常简单的单一半街下注游戏,不允许弃牌。玩家X必须过牌,并且跟注Y的下注,如果Y选择下注的话。当没有弃牌选项时,这类游戏的底池大小就无所谓了。
X没有需要决定的。Y的策略包含一个简单的决定——下注还是不下注?Y知道X的应对,也就是会跟注任何下注,所以Y可以简单地下注那些正期望和0期望的手牌,过牌那些负期望的牌。
我们会经常建立如下图的表格,来显示各种结果
Y下注手牌y期望是:

回忆之前X的手牌是均匀分布的,所以桌上每条打法的概率等于X手牌间隔的大小。
< Y, 下注> = p(X牌更好)(-1)+p(X牌更差)(+1)
< Y, 下注> = (y – 0)(-1) + ( 1 – y )( 1 )
< Y, 下注> = 1 – 2y
现在我们找到了所有Y的期望大于0的部分,
1 – 2y > 0
y <= ½
所以Y应该下注他最好的一半牌;X不得不跟注。当X手牌范围在[0,1/2]之间,Y刚好总体打平,而当X处于[1/2,1]之间,Y赢下1。
从图像上来看就是这样,
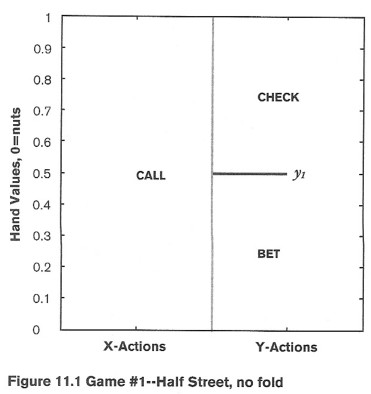
Y在一半的时候下注,其中半数的时候赢下底池,从而使得整个游戏的赢率是1/4。
这个没有弃牌的游戏是个非常简单的版本,但是他介绍了[0,1]游戏,并且展示了一些关键原则。其中之一就是,对手不需要做任何决策,那么我们只要简单地针对他的静态策略最大化期望就是最优的策略。其次是如果你的范围和对手相似,你也不会被加注,因为对手永远都是跟注,所以这里你需要下注一半的手牌。我们会在许多无法加注的情况看到类似的结论。
牌例 11.3 [0,1]游戏 #2
在之前的游戏里,我们订了一个很特殊的规则,一半扑克游戏里很少见——那就是不允许弃牌。我们发现如果在“不弃牌”游戏里,也就没有诈唬——也就意味着Y的下注范围就是简单的上半部分顶端范围。扑克游戏经常被人们认为是诈唬的游戏,那么我们把注意力转移到对手可以弃牌的版本。
[0,1]游戏 #2与之前的版本完全一致,除了X是可以弃牌的。因此这里底池大小就会变得相关,X的决定会基于他手牌跟注的收益。我们继续用惯例(限注游戏里的)底池大小为P,对手下注大小为1。
在第一个游戏里,我们已经总结了Y的策略就是一个阈值y;然而随着游戏变得复杂,我们会有更多的阈值。我们这里会用类似的变量来代表这些值。
· xn是策略之间的阈值,即第n次下注和(n-1)次价值下注之间(当允许更多下注和过牌=加注时,我们会用到x2,举例就是过牌和下注最初的阈值)。
· x0是一个特殊的阈值(在诈唬和过牌之间)
· xn*是跟注第n次下注和弃牌之间的阈值
通过这些规则的第一条,可以知道游戏#1里y的策略就是y1,因为Y用高于这个数值的手牌下注。y0值在这里不存在,也可以被认为是1。因为X不得不总是跟注,所以x1*也是1。
在游戏#2里,X实际上有一个策略,由一个单独的阈值x1*构成,把X的范围分为跟注范围和弃牌范围。X的跟注范围就是[0, x1*],而弃牌范围就是[x1*,1]。
我们可以得到Y的策略会包含一些诈唬:
如果X和Y都玩得最优,那么x1*就是一个在面对Y的策略最大化期望的值。我们看一下,如果Y使用类似游戏#1里的策略,也就是下注0到y1,过牌y1到1。
X最好的应对是跟注那些对于Y的范围有正赢率的牌。当X的赢率为正,此时的x1*就是我们的跟注阈值。
X的赢率是由他的跟注阈值所决定,如果他在x的时候跟注,当Y是在y1和x1*之间,他会获胜并且赢下底池,而当Y在0到y1之间,他会失利,所以他的综合赢率是,
< X > = (获胜时底池大小)(获胜几率)- (下注量)(失败几率)
< X > = ( P + 1 )( y1 – x1*) – 1 (x1*)
当这个值为正数时,他会跟注。
( P + 1 )( y1 – x1*) – 1 (x1*) > 0
( P + 1 )( y1 ) – (P + 2)(x1*) > 0
x1* > y1 ( P + 1 ) / ( P + 2)
所以X会跟注Y一部分的下注,比例是( P + 1 ) / ( P + 2)
直观来说,这是合理的。我们假设底池是1,那么这就是一个底池下注。X需要跟注1/3的好牌。这里阈值就是0到y1的2/3。
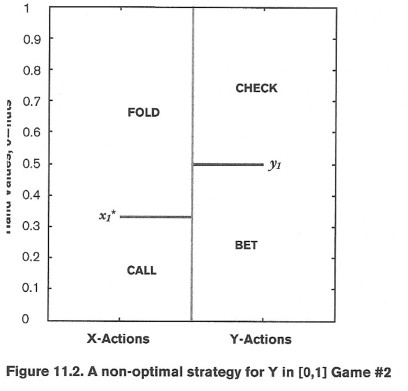
然而,当X这么打的时候,X可以通过过牌x1到y1的牌,并诈唬同样数量接近1的手牌,实现单边地增加赢率。这样做可以增加那些诈唬的赢率,因为X相对于[x1,y1] 而言更多弃掉了那些可以赢诈唬的牌。
因为Y可以通过改变策略来单边提高赢率,那么他的策略一定不是最优的。但是假设是Y的策略已经是最优了,所以这里矛盾,可以得出Y不能只价值下注,必须有一个诈唬范围。
我们可以用如下办法参数化Y的策略:
Y下注一个强范围从0到y1
Y过牌中等范围y1到y0
Y下注最差的范围从y0到1
我们同样也猜测这个参数化里x1*在y1右侧
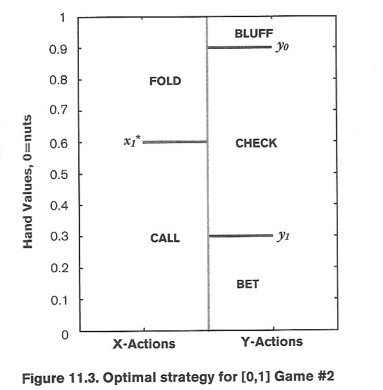
我们知道如果X和Y都在使用最优策略,那么在x1*,X的跟注和弃牌将会无差别。
x1*点的无差别(X的跟注和弃牌无差别)

注意到我们忽略了Y手牌上y1到y0的范围,因为着些牌他没有下注,所以我们还不需要做决定。这里乘积一栏的和一定是相等的——因为他们就是Y所有手牌的加权平均赢率。
-y1 + ( P + 1 )( 1 – y0 ) = 0
y1 = ( P + 1 )( 1 – y0 )
1 – y0 = y1 (1/( P + 1 ))
1 – y0 = α y1
在我们参数化过程中,1 – y0代表了诈唬范围的长度,正如y1代表的是价值下注的数量。这两个数量的关系就像先知游戏里的一样——价值下注和诈唬的比例还是α。
我们可以看下Y两个阈值之间的无差别。
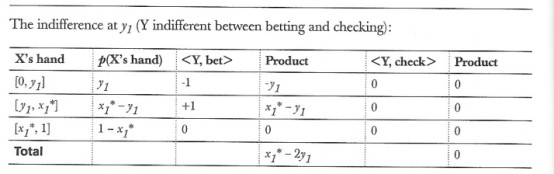
使期望值为0:
x1* – 2 y1 = 0
y1 = x1*/2

P * y0 – ( P + 1 ) x1* = 0
回顾之前公式11-3 1 – y0 = α y1
P * ( 1 – α y1 ) – ( P + 1 ) x1* = 0
x1* = P / ( P + 1 ) ( 1 – α y1 )
而(1 – α ) = P / (P + 1)
x1* = (1 – α ) ( 1 – α y1 )
这个结果也非常重要,因为他决定了在后续范围里跟注的比例。为了让Y的诈唬无差别,X必须跟注一部分可以赢诈唬的牌,这个比例是P/(P+1) 或者是 1 – α。换个说法,我们可以说X要弃掉手中可以赢诈唬里α的牌,从而让Y的诈唬无差别。
将前面3个公式融合在一起,我们就得出了这个游戏的解法:

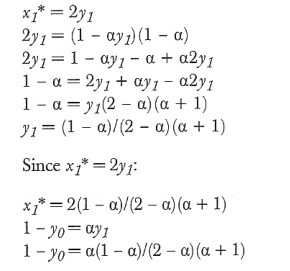
这个游戏是最早由John Von Neumann和Oskar Morganstern在他们著作Game Theory and Economic Behavior(1944)里解决的。
我们能看到这个游戏里一些重要的地方。首先,我们发现X弃牌的选项改变了Y策略的基本结构。在游戏#1里,Y只是简单地价值下注最好的手牌。而在游戏#2里,如果Y使用之前的策略,那么X可以简单地弃掉弱牌,使Y无法获利。那么Y的应对就是开始用最差的牌进行诈唬,迫使X跟注一定数量的牌。
在这个游戏里,我们发现α 也起了明显作用。就像在先知游戏里一样,X弃掉手牌里可以赢诈唬的α 部分,使Y的诈唬无差别,而Y诈唬α的牌使得X的跟注[y1,y0]之间的手牌无差别。
第三个重点如下:诈唬的价值是多少?在先知游戏里,答案是0;如果Y过牌,他只是简单地损失这个底池。在这个游戏里,答案没有那么简单。在y0,Y的诈唬和过牌无差别,这就意味着这个情况和先知游戏是一样的(从摊牌前的角度而言)。但是比如说在1或者y0的时候, Y诈唬的赢率是一样的(因为X只会跟注高于x1*的牌)。所以Y在1的时候诈唬并不是无差别的——实际上,对于那些比y0更差的手牌而言,诈唬增加了他们的赢率。
在这章里,我们展示了两种非常简单的半街游戏和一个稍微复杂一点的。在先知游戏里,我们看到先知玩家的诈唬和价值下注有一个最优的精准点,而对手可以调整弃牌和跟注的比例来使先知玩家的诈唬无差别。在[0,1]游戏#1里,我们介绍了[0,1]游戏的分布并且看到了当一个玩家没有策略选项时,另一个玩家如何简单地最大化赢率。在[0,1]游戏#2里,我们看到了一个类似的模式,下注最好的和最差的手牌,也看到了诈唬如何影响跟注比例阈值,并且迫使X跟注比Y价值下注更差的牌。
重要概念:
· 最优策略中的价值下注和诈唬在半街游戏中是相关的,比例α = 1/(P+1)。通过诈唬这个比例,下注者让跟注者的行为无差别。
· Α 同时也是X在半街游戏中的恰当弃牌比例。通过弃牌这部分,可以是下注者的诈唬无差别。
· 当一个玩家没有策略选项时,对手只需要简单最大化期望值。
· 适当平衡价值下注和诈唬保证了玩家无论对手如何调整都可以榨取价值;如果他过度弃牌,下注者通过诈唬得利;反之,下注者通过价值下注得利。
· 最优策略不总是使诈唬无差别;只是在阈值手牌完全独立时。通常最差的诈唬有着正价值。(相较于过牌而言)
打德州就到蜗牛GG扑克
GGPUKE 摩拳擦掌,聚焦中国!
为中国地区玩家提供安全可靠的游戏环境,打造在线竞技扑克平台
提供喜爱德州比赛的用户们一个新的竞技之路,同時,带给中国用户更多特殊礼遇。
GG扑克官方注册网址:www.ggp666.com
 蜗牛扑克官方-GG扑克
蜗牛扑克官方-GG扑克