德州扑克贝叶斯统计量（上）

蜗牛扑克allnewpoker『www.allnew366.com』亚洲唯一代理,注册登陆游戏访问更快,存提款更加方便,提供安卓苹果APP客户端下载,合法安全稳定,在线中文客服为您服务

发布时间：2021-02-07 文章来源：蜗牛扑克

回想一下在本章较早的阶段中我们讨论过的一个总共打了16900手牌的扑克玩家有以下统计数据：

赢率‾x=1.15bb/100手；

标准差s=2.1bb/手。

我们考虑过一些基于可观察到的信息来猜测这个玩家“真实”赢率的观点。通过经典统计学的方法，我们得出这个牌手的赢率的极大似然估计量为1.15bb/100手，并且其95%的置信区间为[-2.07bb/100手，4.37bb/100手]。这些结论是基于我们对于这个牌手的赢率分布没有任何附加信息的假设下得出的。

但是，假设我们猜测一个赢率的概率分布，并且尝试应用贝叶斯定理分析赢率的概率分布和牌手输出结果，来做一个更精确的估计。为了做到这一点，我们必须首先提出一个关于这个选手总体赢率分布的一个假说。假设这个玩家是从一个常客玩家总体中随机挑选出来的。那么，这个分布，也就是称之为先验概率分布的形状是什么样的呢？

这个分布大概长什么样不是很容易猜测的——事实上，我们不可能掌握所有常客玩家的游戏牌局结果。但我们可以简化和估计，希望我们的赢率的概率分布通过从真实赢率中提取的信息来尽可能地接近真实赢率。假设我们这位牌手混合玩$10-$20，$30-$60的游戏，那么我们可以估计出这个游戏抽水大概为$3-$4每手，或者0.1bb/手。将抽水大概平均分配给每个玩家的话，我们认为抽水对每个玩家的影响大概是0.01bb/手，或者说1bb/100手。

这意味着总体所有牌手的分布的均值，与这个值的相反数相等，因为这恰好是这个游戏的净抽水收入。假设我们有一个服从正态分布的赢率，并且估计赢率的标准差为0.015bb/手。这些假设会使得68%的玩家的赢率在-2.5bb/100手到0.5bb/100手之间，而95%的玩家的赢率在-4bb/100手到2bb/100手之间。这应该与你的直觉相符——如果不是的话，这些数字可以帮助我们在不变化估计进程的情况下，考虑调整不同的假设。

为了简化估计，我们用一个离散分布来粗略地替代之前假设的连续正态分布。我们假设所有扑克玩家的隐含分布如下所示：

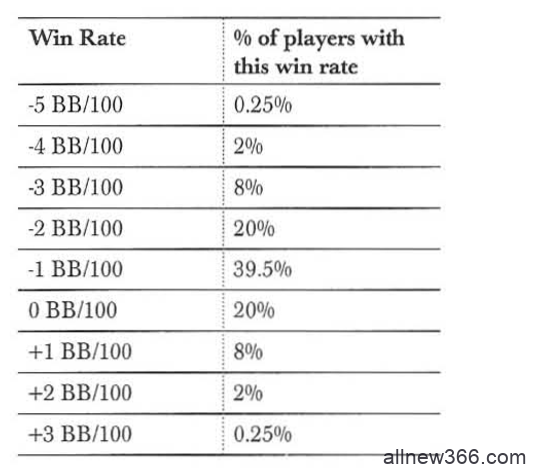
现在我们有了一个对赢率的先验分布，我们可以应用贝叶斯定理解决这个问题。对每个人的赢率，我们如下计算：

事件A=被调查的牌手的赢率是1.15。

事件B=这个牌手的赢率的先验值就是其真实值。

我们不能直接得出这个牌手赢率恰好是1.15的概率（因为其分布是一个连续分布）。但我们可以通过计算概率分布落在1.14到1.16之间的概率来大概估算一下这个值。回想一下之前提到的样本的标准差为1.61个大盲每手。P(A|‾B)可以简单地通过计算P(A|B)的加权平均值来得到。从下面的概率表中：

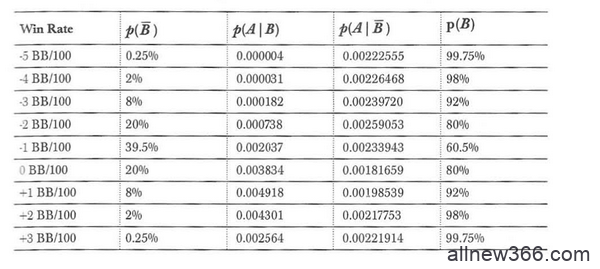
（注：原书上似乎是把P（‾B)和P(B)这两列搞反了）

应用贝叶斯定理我们有：

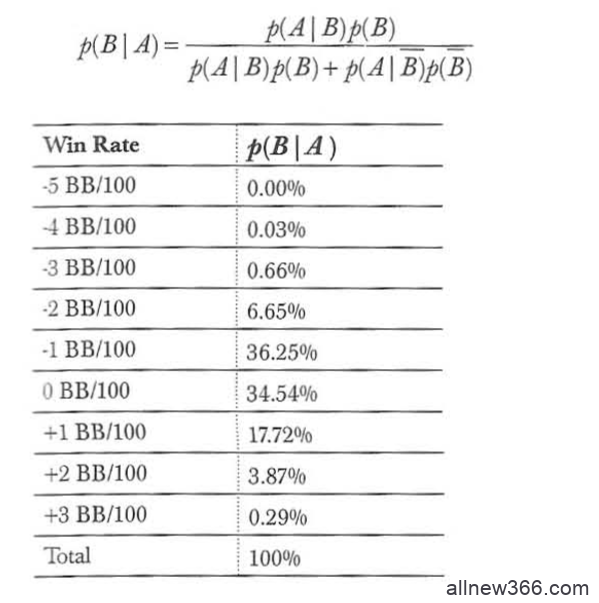
打德州就到蜗牛GG扑克

GGPUKE 摩拳擦掌，聚焦中国!
为中国地区玩家提供安全可靠的游戏环境，打造在线竞技扑克平台
提供喜爱德州比赛的用户们一个新的竞技之路，同時，带给中国用户更多特殊礼遇。

GG扑克官方注册网址：www.ggp666.com